Movement Control of Three Omni-Wheels Robot using Pole Placement State Feedback and PID Control

Swadexi Istiqphara 1,*, Anisa Ulya Darajat 2, Fahmizal 3, Mohammad Farhan Ferdous 4

1 Department of Electrical Engineering, Institut Teknologi Sumatera, Lampung, Indonesia

2 Department of Electrical Engineering, Universitas Lampung, Lampung, Indonesia

3 Department of Electrical Engineering and Informatics, Vocational College Universitas Gadjah Mada, Yogyakarta, Indonesia

4 Chairman & Founder, Japan-Bangladesh Robotics and Advanced Technology Research Center (JBRATRC), Fukui, Japan

Email: 1 swadexi.istiqphara@el.itera.ac.id, 2 anisa.ulya@eng.unila.ac.id, 3 fahmizal@ugm.ac.id, 

4 farhan.ferdous2019@gmail.com 

*Corresponding Author

Abstract—Omni wheels robot have high efficiency in robot movement, but also have its own challenges in controlling this robot, especially robots with three omni wheels (3WD). This paper proposes a robot control system using the pole placement state feedback method to control the inner loop which controls the body reference speed, and PID method is used to control the outer loop which controls the robot's position in world coordinates. The results obtained using computer simulations show that the proposed method is able to control the robot's position in world coordinates even though there is an overshoot of 5- 10% on X and yaw axis, however the Y axis performance is overshoot more than 100% because of coupled effect thats still cannot be eliminated.

Keywords—omni wheels, pole placement, state feedback, robot, PID, control system

1. Introduction

Robot technology is currently growing rapidly because of its increasing benefits in everyday life. The popularity of robots is increasing because of their popularity which is able to be in various environmental conditions [1]. Robots, which initially consisted of only mechanical systems, are now developing into three components: electronics, mechanics, and programming or brainware. Robots have various types based on how they move, using legs (humanoid) [2], wheels or using propellers to fly [3]. One type of robot that will be proposed in this manuscript is the omni wheels robot.

The omni-directional wheels robot [4] or can be mentioned as omni-wheels robot is a type of wheeled robot, this robot use wheels that not only move one axis of movement (1DOF), but uses wheels that have two axes of movement (2DOF) as shown in Fig. 1. Due to its flexibility in movement, the omniwheel robot can move multidirectional on X-Y axis with only three wheels. However, because it only has three wheels, controlling the omni wheel robot is a challenge for researcher. Omni-wheels technology has also been widely applied in industry [5]-[7].

Related Research of the omni wheel robot has been carried out as in [8] which discusses the increase in stability of the omniwheels robot which is usually influenced by various factors including the shape of the wheel which consists of small wheels that disturb the stability, the results obtained show that the robot is able to move more stably. On [9] proposes to increase the navigation ability of the omni-wheeled robot by adding an optical sensor capable of detecting obstacles so that the robot can avoid these obstacles. Omni robot modeling is also widely carried out as in [10]-[12].

1. Omni wheels movement

Research related to other robot control systems such as in [13] which uses a nonlinear predictive control model for tracking the robot's position. Research on robot movement using a microcontroller device was also carried out for position tracking on a 4wd omni-directional robot [14]. Artificial intelligence methods have also been proposed to control 3WD omni wheel robots [11]. Research related to controlling omni wheel robots has also been carried out for a long time as in [15]-[17].

Based on the above literature, basically controlling the omniwheel robot still requires further research in order to obtain various alternative control systems for the omniwheel robot. Therefore, in this study a robot position tracking control system will be proposed using two loop controllers, inner loop control using the pole placement state feedback method and outer loop control using a proportional, integral and derivative (PID) control system.

The use of the pole placement state feedback method aims to control the position with performance based on the desired target pole. so that with this method we can adjust the performance of the robot's movement as desired, whether it moves quickly, namely by using a pole value that has an imaginary axis which causes the robot to move faster but also increases the possibility of overshoot. to determine the target value of this pole can be done by testing each pole [18]-[19]. Meanwhile, the use of PID to control the outer loop is due to the advantages of PID than the others method which does not require a mathematical model to determine the gain coefficients Kp, Ki and Kd [20]-[21].

2. Three Omniwheels Robot Modelling

The design of the three omniwheels robot can be seen in Fig. 2. The robot has wheels that are 120 degrees apart from one another.

2. 3WD omni-wheeled Robot Design

It can be seen that the two coordinates used as a frame of reference for the robot's movement, body coordinates and world coordinates. The speed at the body coordinates is expressed by Vbx, Vby and ω. While the speed at world  coordinates is expressed by Vx, Vy and ω. For the transformation from body coordinates to world coordinates, the following equation is used (1).

Meanwhile, the transformation from world coordinates to body coordinates is expressed on (2)

The equation for the dynamics model of the omniwheels robot stated on (3) [22].

where

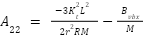
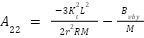
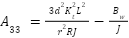
where he variable description is available on Table 1.

3. Proposed method

The method proposed in this paper consists of two control loops which are respectively used to control the inner and outer loop. The diagram of control system used in this paper is shown in Fig. 3.

3. The proposed control system block diagram

1. Inner Loop Control using Pole Placement State Feedback

Inner loop control is used to control the speed at body coordinates. The method used in the inner loop is pole placement state feedback using the model equation in (3). To obtain the gain K, a target pole is needed which is the desired performance. The control law equation using the pole placement state feedback can be seen in (4).

The problem that must be solved in designing a control system using pole placement state feedback is to find the gain K so that state X can move with the specified pole P characteristic. So that the closed loop equation of the system becomes as in (5).

K is pole placement controller gain that can be found using algorithm proposed by [23] and implemented on the following python command in python control system library.

2. Outer Loop Controller Using PID

Proportional Integral and Derivative (PID) is control system approach that has been used in major industries in the world. PID is widely used because it is easy to operate and also does not use model to derive the control law. In this study, the use of PID in controlling the inner loop is less effective than pole placement state feedback. However, the PID method is easier to use in outer loop control because this method does not require state equality as in pole placement state feedback. The PID control system equation that is applied to control the motion of the three-wheeled omni robot is shown in (6).

where u is control input, Kp is proportional constant, Ki is Integral Constant ,  Kd is Derivative Constant, N is filter coefficient and error e is the difference of Target T and Actual Yout as shown in (7)

4. Results and discussion

Control system experiments are carried out using online computer simulations with model parameters as shown in the Table 1.

1. Model Parameters [22]

The simulation is carried out with two types of references or target of positions in cartesian coordinates or earth coordinates that must be achieved by the robot. The two types of references are setpoint and trajectory. Experiments using a target setpoint were carried out to see the performance of the omniwheels robot in achieving a fixed reference and being in a position far from its current position. while the trajectory experiment was carried out to see the robot's performance in following a reference signal that changes every time.

3. Setpoint Experiment

Based on the model equation in (3) and with the model parameters in Table 1, pole placement Gain K can be calculated with the target pole 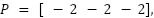 and it is obtained :

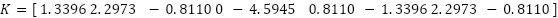
The value of reference gain 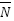which is the gain that strengthens the setpoint to match the Gain K is

And the PID used in this simulation is only use Proprotional control and the constant is  on Table 2.  

2. P gain constant value

The simulation time is set for 50 seconds to simulate the robot's movement in reaching the given target position of XT = 2.0m, YT = 1.0m and ThetaT = 1.0 rad. The simulation  results obtained by using the above controller configuration is shown in Fig. 4-Fig. 9.

4. Setpoint Tracking of X axis

5. Velocity on X axis of body coordinate

In Fig. 4 can be seen the performance of the PID control system in tracking the robot's position on the X axis, the robot is able to reach a target position of 1 meters within 15 seconds with a maximum speed of 0.4m/s and continues to slow down when approaching the target as can be seen in Fig. 5.

6. Setpoint Tracking of X axis

In Fig. 6 and Fig. 7 is the Y Axis Movement of robot and velocity tracking. It can be seen that the performance of proportional control is still not optimal, this is because there is an oscillating movement in the transient response when heading for the setpoint or target. This error indicates the need for improvement on the proportional gain. Meanwhile, the pole placement control system shows good results in tracking setpoints.

7. Velocity on Y axis of body coordinate

8. Setpoint Tracking of yaw angle (θ) axis

9. Velocity of Yaw Angle (

Fig. 8 and Fig. 9 show the movement on the yaw axis(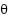) or the direction of the robot. The yaw target given is 1 rad, and from this movement the robot is able to move to the specified yaw angle with good results for 10 seconds without overshoot.

4. Controller Adjustment

Based on the results of the first experiment, it shows that there are weaknesses in the proportional controller, namely the speed of reaching the target for 10-15 seconds which is still relatively long, and there are also oscillations during the transient process. In this second experiment, adjustments will be made taking into account the integral and derivative gains to overcome these two problems.

Adjustment value of the PID controller can be seen in Table 3. and the simulation results carried out with a simulation time of 20 seconds can be seen in Fig. 10 – Fig. 12. It can be seen that the movement on the X and yaw axes shows an increase in performance, namely being faster in reaching the setpoint even though there is an overshoot of 5-10%. However, movement on the Y axis is still a problem, control on the Y axis is still difficult to do to speed up system response, this can be seen in Fig. 11.

3. PID Gain Constant

10. X axis movement on 2nd experiment

11. Y axis movement on 2nd experiment

That there is a very large overshoot exceeding 100% with a steady state time speed of 10 seconds. If the controller gain value is increased, it will increase the overshoot, and if it is reduced, it will slow down the system response. This poor system response can be caused by the complexity of the robot when it moves more than 2 axes. Fig. 12. Yaw Axis movement on 2nd experiment can be seen in Fig. 12.

12. Yaw Axis movement on 2nd experiment

5. Conclusion

This paper proposes two methods for controlling the omniwheel robot, the pole placement state feedback method is used to control the inner loop, while the PID is used to control the outer loop. Based on computer simulation results, the proposed pole placement control system is capable of controlling the movement of the inner loop (velocity control) on the omni wheels robot. While the PID controller is able to control the robot on the X and yaw axis movements with a steady state speed of 1-2 seconds with a target distance of 2 meters, while on the Y axis controller, the PID still cannot work properly with an overshoot of more than 100%, although slow steady state time of 10 seconds, this is due to the influence of the coupled input signals on the robot wheels. This research still needs to be carried out further in order to produce a control system that is more robust and has a faster time to reach the target.

References

1. S. Barbuto and J. Stein, “Rehabilitation Robotics for Stroke,” Stroke Rehabil., pp. 235–247, 2019, https://doi.org/10.1016/B978-0-323-55381-0.00017-2.
2. T. Nomura, “Robots and Gender,” Princ. Gender-Specific Med. Gend. Genomic Era Third Ed., pp. 695–703, 2017, https://doi.org/10.1016/B978-0-12-803506-1.00042-5.
3. R. Konomura and K. Hori, "Phenox: Zynq 7000 based quadcopter robot," 2014 International Conference on ReConFigurable Computing and FPGAs (ReConFig14), pp. 1-6, 2014, https://doi.org/10.1109/ReConFig.2014.7032546.
4. H. Taheri and C. X. Zhao, “Omnidirectional mobile robots, mechanisms and navigation approaches,” Mech. Mach. Theory, vol. 153, p. 103958, 2020, https://doi.org/10.1016/j.mechmachtheory.2020.103958.
5. T. Peng, J. Qian, B. Zi, J. Liu, and X. Wang, “Mechanical Design and Control System of an Omni-directional Mobile Robot for Material Conveying,” Procedia CIRP, vol. 56, pp. 412–415, 2016, https://doi.org/10.1016/j.procir.2016.10.068.

6. S. Guo, Q. Diao, and F. Xi, “Vision Based Navigation for Omni-directional Mobile Industrial Robot,” Procedia Comput. Sci., vol. 105, pp. 20–26, 2017, https://doi.org/10.1016/j.procs.2017.01.182.
7. M. Waibel, “Omniwheels Gaining Popularity in Robotics," IEEE Spectrum, 2010, https://spectrum.ieee.org/omniwheels.
8. C. Ye, D. Zhao, S. Yu, C. Jiang, and P. Li, “Stability improvement of mobile robot with mutative driving axial distance omni-directional wheels,” 2018 IEEE Int. Conf. Real-Time Comput. Robot. RCAR 2018, pp. 325–330, 2019, https://doi.org/10.1109/RCAR.2018.8621658.
9. N. Z. Zailan, M. A. Ayob, A. S. Sadun, H. M. Poad, R. Sawarno, and N. Rohaziat, “Obstacle Avoidance of a 3WD Omni-Wheel Mobile Robot in Webots Environment,” 2021 IEEE 11th Int. Conf. Syst. Eng. Technol. ICSET 2021 - Proc., pp. 143–146, 2021, https://doi.org/10.1109/ICSET53708.2021.9612576.
10. C. W. Wu, Z. W. Qiu, Y. H. Wang, P. H. Hsu, and C. K. Hwang, “Modeling of a spherical robot driven by Omni wheels,” Proc. - Int. Conf. Mach. Learn. Cybern., vol. 3, pp. 1256–1260, 2011, https://doi.org/10.1109/ICMLC.2011.6016887.

11. M. A. Saleh, M. Soliman, H. H. Ammar and M. A. W. Shalaby, "Modeling and control of 3-omni wheel Robot using PSO optimization and Neural Network," 2020 International Conference on Control, Automation and Diagnosis (ICCAD), pp. 1-6, 2020, https://doi.org/10.1109/ICCAD49821.2020.9260509.
12. B.-J. Yi and W. K. Kim, “Kinematic Modeling of Omni-Directional Mobile Robots as Parallel Manipulator,” IFAC Proc. Vol., vol. 34, no. 4, pp. 165–171, 2001, https://doi.org/10.1016/S1474-6670(17)34290-8.
13. A. S. Conceição, H. P. Oliveira, A. S. Silva, D. Oliveira, and A. P. Moreira, “A nonlinear model predictive control of an omni-directional mobile robot,” IEEE Int. Symp. Ind. Electron., pp. 2161–2166, 2007, https://doi.org/10.1109/ISIE.2007.4374943.
14. M. Alfiyan and R. D. Puriyanto, “Mecanum 4 Omni Wheel Directional Robot Design System Using PID Method,” J. Fuzzy Syst. Control, vol. 1, no. 1, pp. 6–13, 2023, https://doi.org/10.59247/jfsc.v1i1.27.
15. S. L. Dickerson and B. D. Lapin, "Control of an omni-directional robotic vehicle with Mecanum wheels," NTC '91 - National Telesystems Conference Proceedings, pp. 323-328, 1991, https://doi.org/10.1109/NTC.1991.148039.

16. H. Asama, M. Sato, L. Bogoni, H. Kaetsu, A. Matsumoto, and I. Endo, “Development of an omni-directional mobile robot with 3 DOF decoupling drive mechanism,” Proc. - IEEE Int. Conf. Robot. Autom., vol. 2, pp. 1925–1930, 1995, https://doi.org/10.1109/ROBOT.1995.525546.
17. Y. Mori, E. Nakano, T. Takahashi, and K. Takayama, “Study on the mechanism and control of omni-directional vehicle,” IEEE Int. Conf. Intell. Robot. Syst., vol. 1, pp. 52–59, 1996, https://doi.org/10.1109/IROS.1996.570629.
18. K. Ogata, “Modern Control Engineering,” Prentice hall, 2010, https://ds.amu.edu.et/xmlui/bitstream/handle/123456789/17552 
19. Fahmizal, J. T. Putra, S. Fatimawardhani, and H. Maghfiroh, “Hydraulic Power System Control using State Feedback Controller (SFC),” J. Fuzzy Syst. Control, vol. 1, no. 1, pp. 28–31, 2023, https://doi.org/10.59247/jfsc.v1i1.30.
20. R. Aisuwarya and Y. Hidayati, “Implementation of ziegler-nichols PID tuning method on stabilizing temperature of hot-water dispenser,” 2019 16th Int. Conf. Qual. Res. QIR 2019 - Int. Symp. Electr. Comput. Eng., 2019, https://doi.org/10.1109/QIR.2019.8898259.

21. J. J. Gude and E. Kahoraho, "Modified Ziegler-Nichols method for fractional PI controllers," 2010 IEEE 15th Conference on Emerging Technologies & Factory Automation (ETFA 2010), pp. 1-5, 2010, https://doi.org/10.1109/ETFA.2010.5641074.
22. H. P. Oliveira, A. J. Sousa, A. P. Moreira, and P. J. Costa, “Dynamical models for omni-directional robots with 3 and 4 wheels,” ICINCO 2008 - Proc. 5th Int. Conf. Informatics Control. Autom. Robot., vol. 2, pp. 189–196, 2008, https://doi.org/10.5220/0001489201890196.
23. A. L. Tits and Y. Yang, “Globally convergent algorithms for robust pole assignment by state feedback,” IEEE Trans. Automat. Contr., vol. 41, no. 10, pp. 1432–1452, 1996, https://doi.org/10.1109/9.539425.